We assume that the energies and momenta involved are nonrelativistic. The de Broglie wavelength is defined as
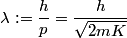 where 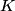 is the kinetic energy of the particle. Initially, is the kinetic energy of the particle. Initially, 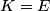 , but after the particle enters the region in which it has a potential energy , but after the particle enters the region in which it has a potential energy 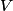 , the kinetic energy becomes , the kinetic energy becomes 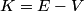 . Therefore, the initial de Broglie wavelength must be multiplied by a factor of . Therefore, the initial de Broglie wavelength must be multiplied by a factor of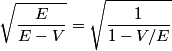 in order to obtain the new de Broglie wavelength. Therefore, the correct answer is (E). |